原理:
设两个有序的子序列(相当于输入序列)放在同一序列中相邻的位置上:array[low..m],array[m + 1..high],先将它们合并到一个局部的暂存序列 temp (相当于输出序列)中,待合并完成后将 temp 复制回 array[low..high]中,从而完成排序。
在具体的合并过程中,设置 i,j 和 p 三个指针,其初值分别指向这三个记录区的起始位置。合并时依次比较 array[i] 和 array[j] 的关键字,取关键字较小(或较大)的记录复制到 temp[p] 中,然后将被复制记录的指针 i 或 j 加 1,以及指向复制位置的指针 p加 1。重复这一过程直至两个输入的子序列有一个已全部复制完毕(不妨称其为空),此时将另一非空的子序列中剩余记录依次复制到 array 中即可
备注:图片原理来源:https://blog.csdn.net/yinjiabin/article/details/8265827/
待排序列(14,12,15,13,11,16)
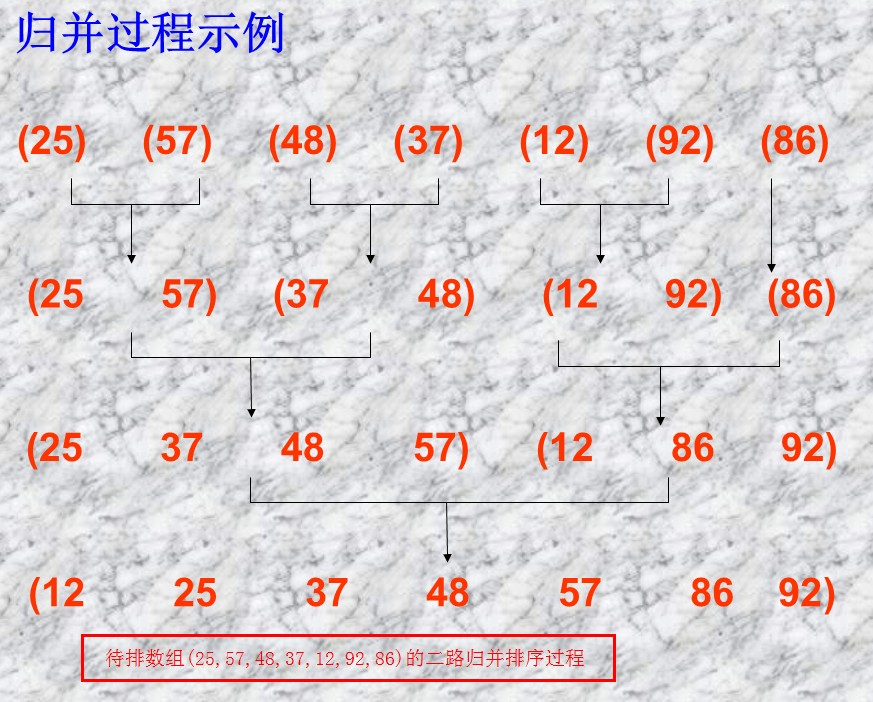
假设我们有一个没有排好序的序列,那么首先我们使用分割的办法将这个序列分割成一个个已经排好序的子序列。然后再利用归并的方法将一个个的子序列合并成排序好的序列。分割和归并的过程可以看下面的图例。
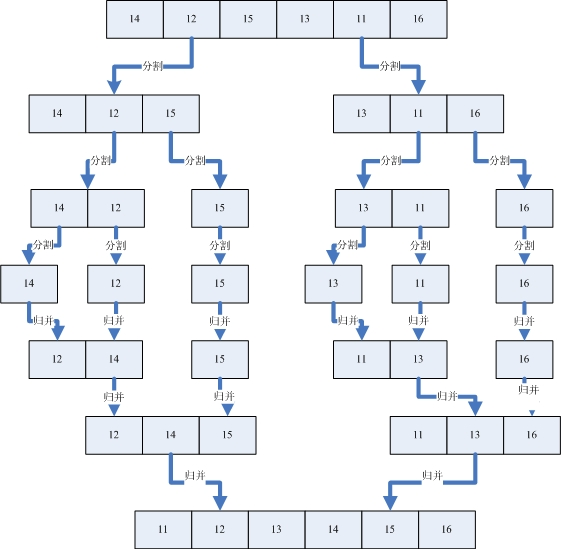
先"分割"再"合并"
从上图可以看出,我们首先把一个未排序的序列从中间分割成2部分,再把2部分分成4部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
测试用例:
#ifndef INC_02_MERGE_SORT_SORTTESTHELPER_H #define INC_02_MERGE_SORT_SORTTESTHELPER_H #include <iostream> #include <algorithm> #include <string> #include <ctime> #include <cassert> using namespace std; SortTestHelper { // 生成有n个元素的随机数组,每个元素的随机范围为[rangeL,rangeR] int *generateRandomArray(int n,int range_l,1)">int range_r) { int *arr = new [n]; srand(time(NULL)); for (int i = 0; i < n; i++) arr[i] = rand() % (range_r - range_l + 1) + range_l; return arr; } 生成一个近乎有序的数组 首先生成一个含有[0...n-1]的完全有序数组,之后随机交换swapTimes对数据 swapTimes定义了数组的无序程度 int *generateNearlyOrderedArray( swapTimes){ [n]; for(0 ; i < n ; i ++ ) arr[i] = i; srand(time(NULL)); for( 0 ; i < swapTimes ; i ++ ){ int posx = rand()%n; int posy = rand()%n; swap( arr[posx],arr[posy] ); } 拷贝整型数组a中的所有元素到一个新的数组,并返回新的数组 int *copyIntArray(int a[],1)"> n){ * 在VS中,copy函数被认为是不安全的,请大家手动写一遍for循环:) copy(a,a+n,arr); 打印arr数组的所有内容 template<typename T> void printArray(T arr[],1)"> n) { ) cout << arr[i] << " "; cout << endl; ; } 判断arr数组是否有序 template<typename T> bool isSorted(T arr[],1)">0; i < n - 1; i++) if (arr[i] > arr[i + 1]) return false; true 测试sort排序算法排序arr数组所得到结果的正确性和算法运行时间 template<typename T> void testSort(const string &sortName,1)">void (*sort)(T[],1)">int),T arr[],1)"> n) { clock_t startTime = clock(); sort(arr,n); clock_t endTime = clock(); cout << sortName << " : " << double(endTime - startTime) / CLOCKS_PER_SEC << s"<<endl; assert(isSorted(arr,n)); ; } }; #endif INC_02_MERGE_SORT_SORTTESTHELPER_H
插入排序(因为等下优化时需要用到):
#ifndef INC_03_MERGE_SORT_ADVANCE_INSERTIONSORT_H #define INC_03_MERGE_SORT_ADVANCE_INSERTIONSORT_H #include <algorithm> std; template<typename T> void insertionSort(T arr[],1)"> n){ 1 ; i < n ; i ++ ) { T e = arr[i]; j; for (j = i; j > 0 && arr[j-1] > e; j--) arr[j] = arr[j-]; arr[j] = e; } ; } 对arr[l...r]范围的数组进行插入排序 template<typename T> int l,1)"> r){ int i = l+1 ; i <= r ; i ++for (j = i; j > l && arr[j-INC_03_MERGE_SORT_ADVANCE_INSERTIONSORT_H
一般归并排序:
#ifndef INC_03_MERGE_SORT_ADVANCE_MERGESORT_H #define INC_03_MERGE_SORT_ADVANCE_MERGESORT_H #include <iostream> 将arr[l...mid]和arr[mid+1...r]两部分进行归并 template<typename T> void __merge(T arr[],1)">int mid,1)"> r){ T aux[r-l+]; int i = l ; i <= r; i ++ ) aux[i-l] = arr[i]; 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1 int i = l,j = mid+; int k = l ; k <= r; k ++ ){ if( i > mid ){ 如果左半部分元素已经全部处理完毕 arr[k] = aux[j-l]; j ++; } else if( j > r ){ 如果右半部分元素已经全部处理完毕 arr[k] = aux[i-l]; i ++if( aux[i-l] < aux[j-l] ) { 左半部分所指元素 < 右半部分所指元素 arr[k] = aux[i-l]; i ++else{ 左半部分所指元素 >= 右半部分所指元素 arr[k] = aux[j-l]; j ++; } } } 递归使用归并排序,对arr[l...r]的范围进行排序 template<typename T> void __mergeSort(T arr[],1)">if( l >= r ) int mid = (l+r)/2; __mergeSort(arr,l,mid); __mergeSort(arr,mid+,r); __merge(arr,mid,r); } template<typename T> void mergeSort(T arr[],1)"> n){ __mergeSort( arr,0,n- ); } INC_03_MERGE_SORT_ADVANCE_MERGESORT_H
优化后的归并排序:
#include <iostream> #include SortTestHelper.hInsertionSort.hMergeSort.h" 使用优化的归并排序算法,1)">void __mergeSort2(T arr[],1)"> 优化2: 对于小规模数组,使用插入排序 if( r - l <= 15 ){ insertionSort(arr,r); ; __mergeSort2(arr,mid); __mergeSort2(arr,r); 优化1: 对于arr[mid] <= arr[mid+1]的情况,不进行merge 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失 if( arr[mid] > arr[mid+] ) __merge(arr,1)">void mergeSort2(T arr[],1)"> n){ __mergeSort2( arr,1)"> main() { int n = 50000 测试1 一般性测试 cout<<Test for random array,size = "<<n<<]endl; int* arr1 = SortTestHelper::generateRandomArray (n,0int* arr2 = SortTestHelper::copyIntArray(arr1,1)">int* arr3 =Insertion SortMerge SortMerge Sort 2delete[] arr1; [] arr2; [] arr3; cout<< 测试2 测试近乎有序的数组 int swapTimes = 10; assert( swapTimes >= ); cout<<Test for nearly ordered array,swap time = "<<swapTimes<<endl; arr1 = SortTestHelper::generateNearlyOrderedArray(n,swapTimes); arr2 =[] arr3; return ; }
测试结果:
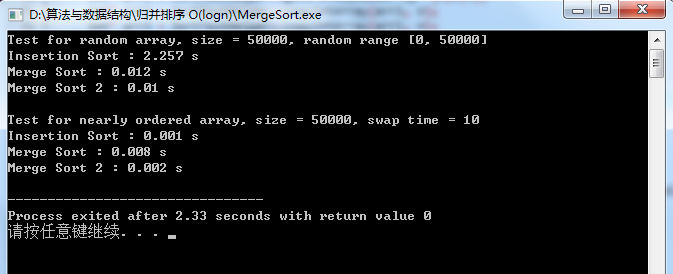
原文链接:/algorithms/997819.html

