插入排序
第一种:交换法
| 8 | 6 | 3 | 2 | 10 | 9 | 11 | 4 | 5 |
第一个元素就不需要考虑了,直接看第二个元素6,因为6<8,所以6与8交换位置得到:
| 6 | 8 | 3 | 2 | 10 | 9 | 11 | 4 | 5 |
在考虑第三个元素3,因为3<8,交换3和8,再比较3和6因为3<6,交换3和6得到:
| 3 | 6 | 8 | 2 | 10 | 9 | 11 | 4 | 5 |
后面以此类推
第二种:复制法:
|51|6|85|6|8|5|4|
| | 6|
将6复制一份,然后比较6之前的元素51
因为6<51,不适合放到当前位置,所以将51向后移动 ,考虑6是不是应该放到前一个位置
|51|51|85|6|8|5|4|
|6 |
因为现在6已经是第0个位置了,所以就放到这个位置。。。。以此类推
和上一个博客一样,将之前的选择排序写到一个 .h 文件中来测试:
测试代码:
1 #ifndef INC_04_INSERTION_SORT_SORTTESTHELPER_H 2 #define INC_04_INSERTION_SORT_SORTTESTHELPER_H 3 #include <iostream> 4 #include <algorithm> 5 #include <string> 6 #include <ctime> 7 #include <cassert> 8 using namespace std; 9 SortTestHelper { 10 // 生成有n个元素的随机数组,每个元素的随机范围为[rangeL,rangeR] 11 int *generateRandomArray(int n,int range_l,1)">int range_r) { 12 int *arr = new [n]; 13 srand(time(NULL)); 14 for (int i = 0; i < n; i++) 15 arr[i] = rand() % (range_r - range_l + 1) + range_l; 16 return arr; 17 } 18 拷贝整型数组a中的所有元素到一个新的数组,并返回新的数组 19 int *copyIntArray(int a[],1)"> n){ 20 21 copy(a,a+n,arr); 22 23 24 打印arr数组的所有内容 25 template<typename T> 26 void printArray(T arr[],1)"> n) { 27 28 cout << arr[i] << " "; 29 cout << endl; 30 31 32 判断arr数组是否有序 33 template<typename T> 34 bool isSorted(T arr[],1)">35 36 0; i < n - 1; i++37 if (arr[i] > arr[i + 1]) 38 return false39 true40 41 测试sort排序算法排序arr数组所得到结果的正确性和算法运行时间 42 template<typename T> 43 void testSort(const string &sortName,1)">void (*sort)(T[],1)">int),T arr[],1)">44 clock_t startTime = clock(); 45 sort(arr,n); 46 clock_t endTime =47 cout << sortName << " : " << double(endTime - startTime) / CLOCKS_PER_SEC << s"<<endl; 48 assert(isSorted(arr,n)); 49 50 51 }; 52 53 #endif
选择排序代码:
#ifndef INC_04_INSERTION_SORT_SELECTIONSORT_H #define INC_04_INSERTION_SORT_SELECTIONSORT_H 5 6 template<typename T> 7 void selectionSort(T arr[],1)"> 8 for(0 ; i < n ; i ++){ 9 int minIndex = i; 10 for( int j = i + 1 ; j < n ; j ++ ) 11 if( arr[j] < arr[minIndex] ) 12 minIndex = j; swap( arr[i],arr[minIndex] ); 14 15 } 16 #endif
#include <iostream> #include <algorithm> #include SortTestHelper.hSelectionSort.h" std; 一,没有优化的插入排序(交换法) /* template<typename T> void insertionSort(T arr[],int n){ //插入排序第一个元素不用考虑 for( int i = 1 ; i < n ; i ++ ) { // 寻找元素arr[i]合适的插入位置 // 写法一: // for( int j = i ; j > 0 ; j-- ) // if( arr[j] < arr[j-1] ) // swap( arr[j],arr[j-1] ); // else // break; // 写法二 : for( int j = i ; j > 0 && arr[j] < arr[j-1] ; j -- ) swap( arr[j],arr[j-1] ); } return; } */ 二,优化后的插入排序 (复制法) 51,6,85,8,5,4 6 将6复制一份,然后比较6之前的元素51 因为6<51,不适合放到当前位置,所以将51向后移动 ,考虑6是不是应该放到前一个位置 6 因为现在6已经是第0个位置了,所以就放到这个位置。。。。以此类推 写法三 : template<typename T> void insertionSort(T arr[],1)"> n){ 1 ; i < n ; i ++ ) { 寻找元素arr[i]合适的插入位置 T e = arr[i]; int j;保存元素e应该插入的位置 for( j = i ; j > 0 && arr[j-1] > e ; j -- ){ arr[j] = arr[j-]; } arr[j] = e; } } 比较SelectionSort和InsertionSort两种排序算法的性能效率 此时, 插入排序比选择排序性能略低 main() { int n = 20000; cout<<Test for random array,size = "<<n<<,random range [0,]endl; int *arr1 = SortTestHelper::generateRandomArray(n,0,1)">3); int *arr2 = SortTestHelper::copyIntArray(arr1,n); SortTestHelper::testSort(Insertion SortSelection Sortdelete[] arr1; [] arr2; cout<<return 0; }
进行测试:
1.首先看一下没有进行优化的[写法一:]插入排序和选择排序性能比较:

2.然后是没有进行优化的[写法二:]插入排序和选择排序性能比较:

可见虽然性能都差不多,但是写法二明显比写法一的代码更漂亮
结论:在随机的,无序的情况下,即是插入排序没有优化但是它的性能依然比选择排序好
3.优化后的插入排序与选择排序比较:
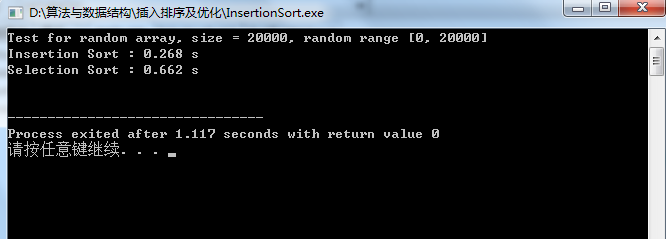
可见此时插入排序的性能远远大于选择排序
原文链接:/algorithms/997812.html

