分治算法
分治算法(Divide And Conquer)是解决规模庞大的问题的很好的思路,它通过降低问题的规模,形成若干个规模更小但形式相同的子问题,进行递归求解。在求解过后,将各个子问题的解合并起来,形成原问题的解。
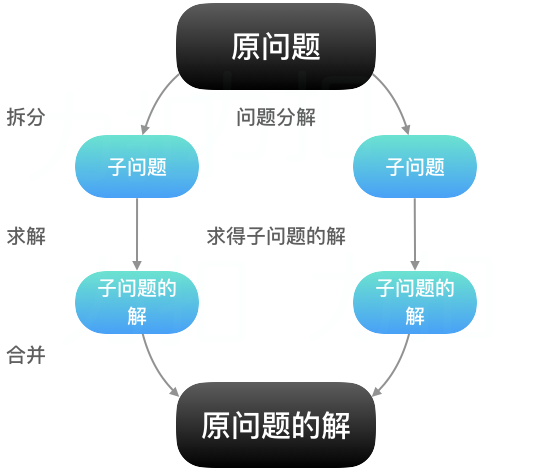
那么它的大致流程主要分成三步:
- 分解(Divide)将大规模的问题分解成若干个规模更小但形式相同的子问题
- 解决(Conquer)如果当前问题的规模足够小,并可以直接解决的话,那么直接解决并返回解。否则,继续进行分解并递归求解分解后的子问题。
- 合并(Merge)将各个子问题合并,最终形成原问题的解。
分治算法一般来说会采用递归法来进行实现,当然利用迭代法(比如for、while)也是可以的。所以,我们往往看到的递归算法从广义上来说都是分治算法。无非就是有些递归算法将问题分解了若干个子问题,然而有些递归算法将问题分解成了一个子问题。
应用场景
- 二分查找
- 合并排序
- 快速排序
- 大整数乘法
- Strassen矩阵乘法
- 棋盘覆盖
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
- 汉诺塔
例子:数列的最大子序列和
给定一个整数数组,找出总和最大的连续数列,并返回总和。
输入: [-2,1,-3,4,-1,2,-5,4]
输出: 6
解释: 连续子数组 [4,1] 的和最大,为 6。
本题比较优的解法是动态规划,我们尝试用分治算法进行解决。
我们把数组分割成两边,那么结果出现的区域,完全在左边、完全在右边、包括中间两个节点的左右两部分
public class Test1617 {
public static void main(String[] args) {
Test1617 test = new Test1617();
int[] nums = {-2,4};
System.out.println(test.maxSubArray(nums));
}
public int maxSubArray(int[] nums) {
if (nums.length == 0) {
return 0;
}
return divide(nums,nums.length-1);
}
private int divide(int[] nums,int left,int right) {
if (left == right) {
return nums[left];
}
int mid = (left + right) >> 1;
// 1.左边最大的子序列
int leftMaxSum = divide(nums,left,mid);
// 2.右边最大的子序列
int rightMaxSum = divide(nums,mid+1,right);
// 3.最大数列和在中间
// 包括中间的,左边部分最大
int sum = nums[mid];
int leftMidSum = sum;
for (int i=mid-1; i>=left; i--) {
sum += nums[i];
leftMidSum = Math.max(leftMidSum,sum);
}
// 包括中间的,右边部分最大
sum = nums[mid+1];
int midRightSum = sum;
for (int i=mid+2; i<=right; i++) {
sum += nums[i];
midRightSum = Math.max(midRightSum,sum);
}
return Math.max(Math.max(leftMaxSum,rightMaxSum),leftMidSum+midRightSum);
}
}

